5 6 Inequalities in Two Triangles and Indirect Proof Continued
- Slides: 20
Download presentation

5 -6 Inequalities in Two Triangles Warm Up Lesson Presentation Lesson Quiz Holt Geometry

5. 6 Indirect Proof and Inequalities in Two Triangles Warm Up 1. Write the angles in order from smallest to largest. X, Z, Y 2. The lengths of two sides of a triangle are 12 cm and 9 cm. Find the range of possible lengths for the third side. 3 cm < s < 21 cm

5. 6 Indirect Proof and Inequalities in Two Triangles Objective Apply inequalities in two triangles.
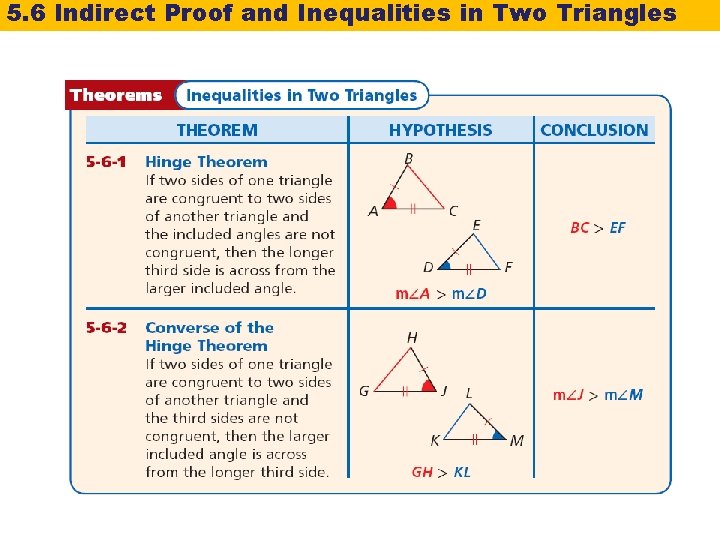
5. 6 Indirect Proof and Inequalities in Two Triangles
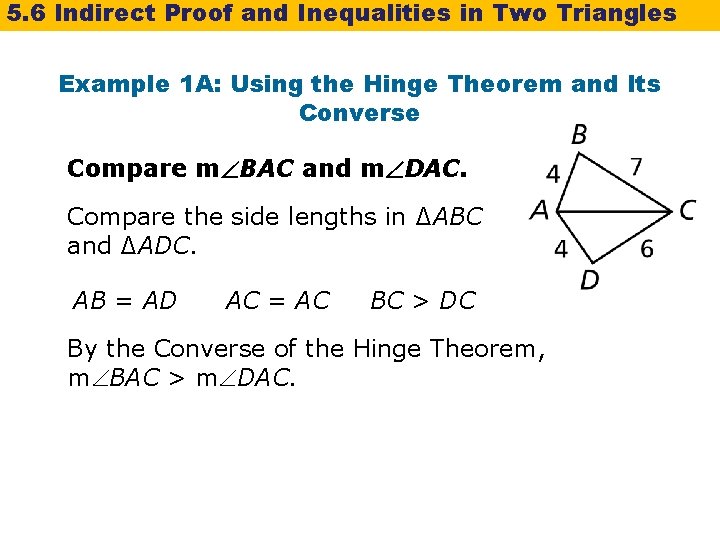
5. 6 Indirect Proof and Inequalities in Two Triangles Example 1 A: Using the Hinge Theorem and Its Converse Compare m BAC and m DAC. Compare the side lengths in ∆ABC and ∆ADC. AB = AD AC = AC BC > DC By the Converse of the Hinge Theorem, m BAC > m DAC.
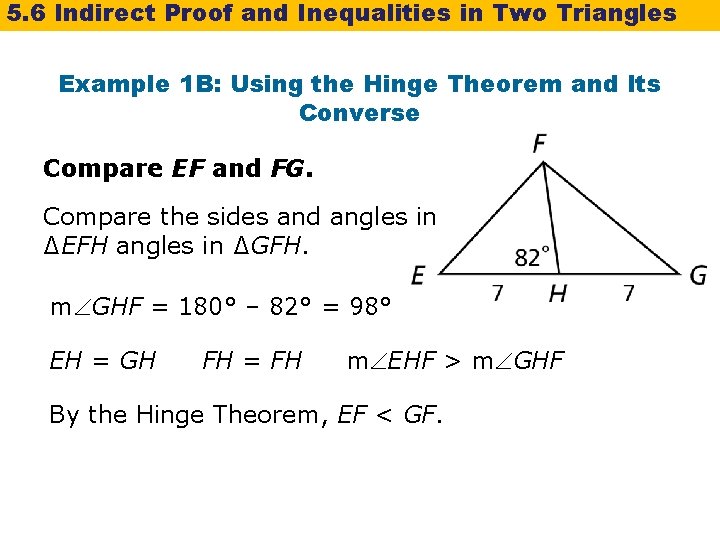
5. 6 Indirect Proof and Inequalities in Two Triangles Example 1 B: Using the Hinge Theorem and Its Converse Compare EF and FG. Compare the sides and angles in ∆EFH angles in ∆GFH. m GHF = 180° – 82° = 98° EH = GH FH = FH m EHF > m GHF By the Hinge Theorem, EF < GF.
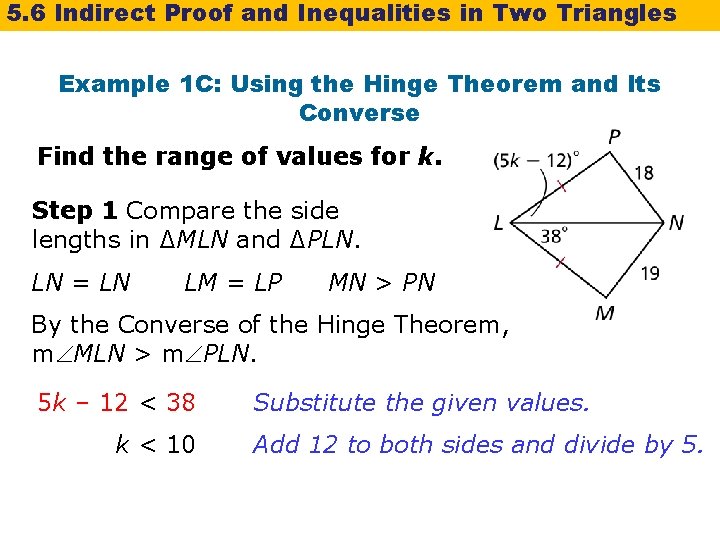
5. 6 Indirect Proof and Inequalities in Two Triangles Example 1 C: Using the Hinge Theorem and Its Converse Find the range of values for k. Step 1 Compare the side lengths in ∆MLN and ∆PLN. LN = LN LM = LP MN > PN By the Converse of the Hinge Theorem, m MLN > m PLN. 5 k – 12 < 38 k < 10 Substitute the given values. Add 12 to both sides and divide by 5.

5. 6 Indirect Proof and Inequalities in Two Triangles Example 1 C Continued Step 2 Since PLN is in a triangle, m PLN > 0°. 5 k – 12 > 0 k < 2. 4 Substitute the given values. Add 12 to both sides and divide by 5. Step 3 Combine the two inequalities. The range of values for k is 2. 4 < k < 10.
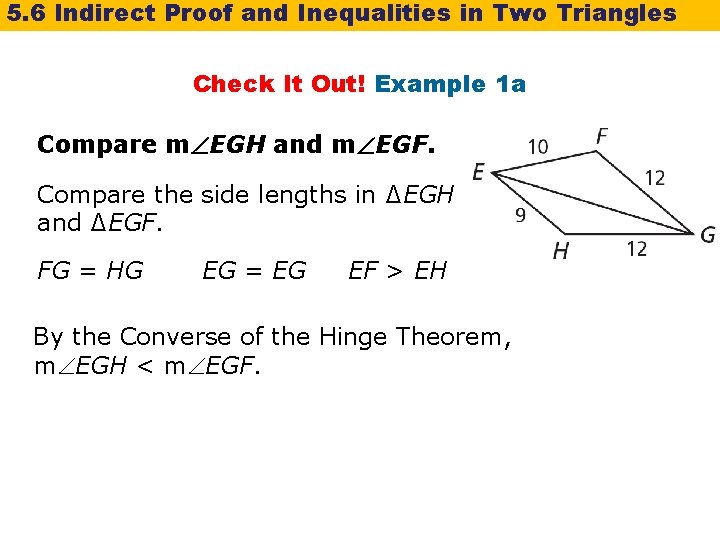
5. 6 Indirect Proof and Inequalities in Two Triangles Check It Out! Example 1 a Compare m EGH and m EGF. Compare the side lengths in ∆EGH and ∆EGF. FG = HG EG = EG EF > EH By the Converse of the Hinge Theorem, m EGH < m EGF.
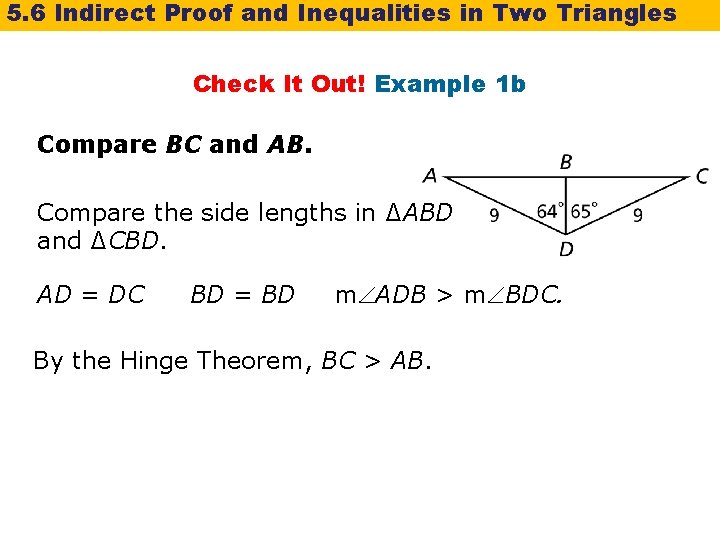
5. 6 Indirect Proof and Inequalities in Two Triangles Check It Out! Example 1 b Compare BC and AB. Compare the side lengths in ∆ABD and ∆CBD. AD = DC BD = BD m ADB > m BDC. By the Hinge Theorem, BC > AB.
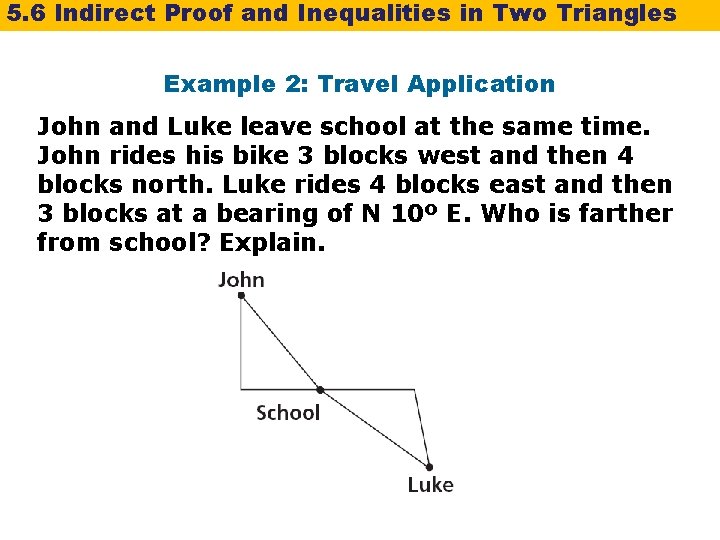
5. 6 Indirect Proof and Inequalities in Two Triangles Example 2: Travel Application John and Luke leave school at the same time. John rides his bike 3 blocks west and then 4 blocks north. Luke rides 4 blocks east and then 3 blocks at a bearing of N 10º E. Who is farther from school? Explain.
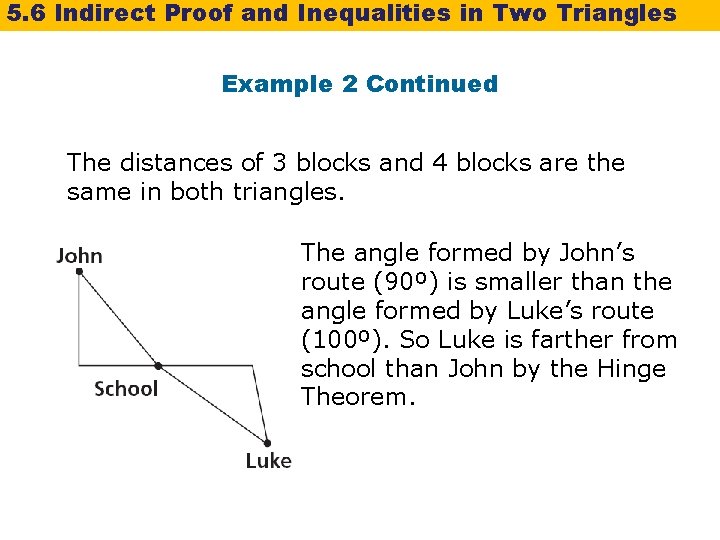
5. 6 Indirect Proof and Inequalities in Two Triangles Example 2 Continued The distances of 3 blocks and 4 blocks are the same in both triangles. The angle formed by John's route (90º) is smaller than the angle formed by Luke's route (100º). So Luke is farther from school than John by the Hinge Theorem.

5. 6 Indirect Proof and Inequalities in Two Triangles Check It Out! Example 2 When the swing ride is at full speed, the chairs are farthest from the base of the swing tower. What can you conclude about the angles of the swings at full speed versus low speed? Explain. The of the swing at full speed is greater than the at low speed because the length of the triangle on the opposite side is the greatest at full swing.
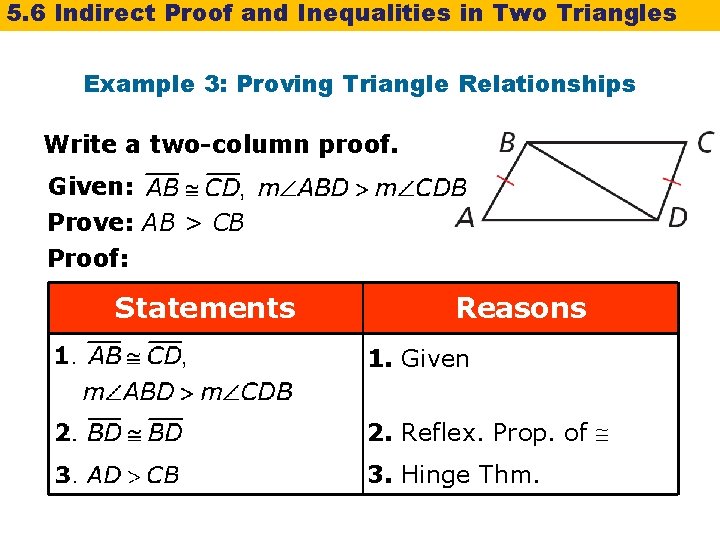
5. 6 Indirect Proof and Inequalities in Two Triangles Example 3: Proving Triangle Relationships Write a two-column proof. Given: Prove: AB > CB Proof: Statements Reasons 1. Given 2. Reflex. Prop. of 3. Hinge Thm.
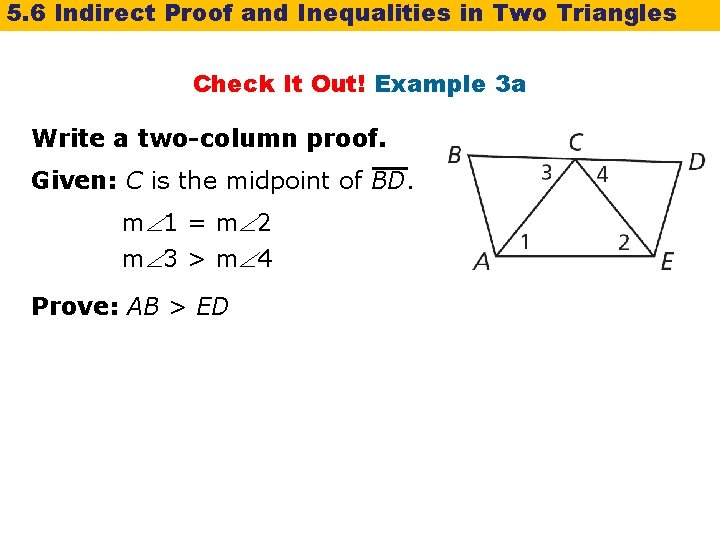
5. 6 Indirect Proof and Inequalities in Two Triangles Check It Out! Example 3 a Write a two-column proof. Given: C is the midpoint of BD. m 1 = m 2 m 3 > m 4 Prove: AB > ED
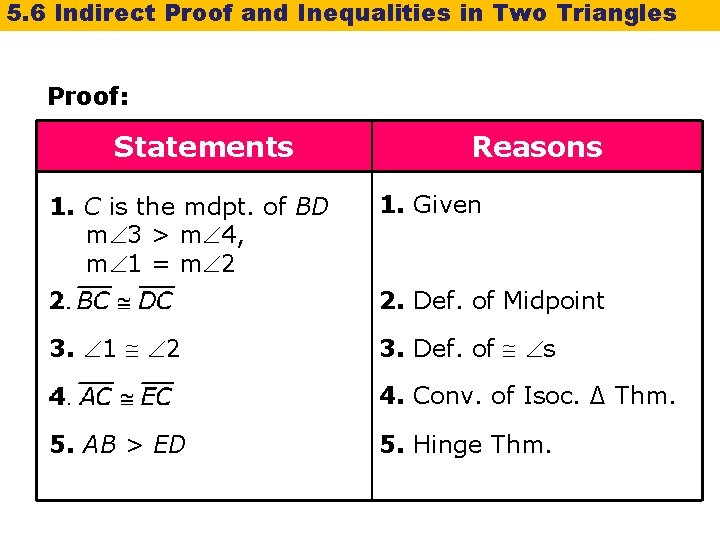
5. 6 Indirect Proof and Inequalities in Two Triangles Proof: Statements 1. C is the mdpt. of BD m 3 > m 4, m 1 = m 2 Reasons 1. Given 2. Def. of Midpoint 3. 1 2 3. Def. of s 4. Conv. of Isoc. ∆ Thm. 5. AB > ED 5. Hinge Thm.

5. 6 Indirect Proof and Inequalities in Two Triangles Check It Out! Example 3 b Write a two-column proof. Given: SRT STR TU > RU Prove: m TSU > m RSU Statements 1. SRT STR TU > RU Reasons 1. Given 2. Conv. of Isoc. Δ Thm. 3. Reflex. Prop. of 4. m TSU > m RSU 4. Conv. of Hinge Thm.
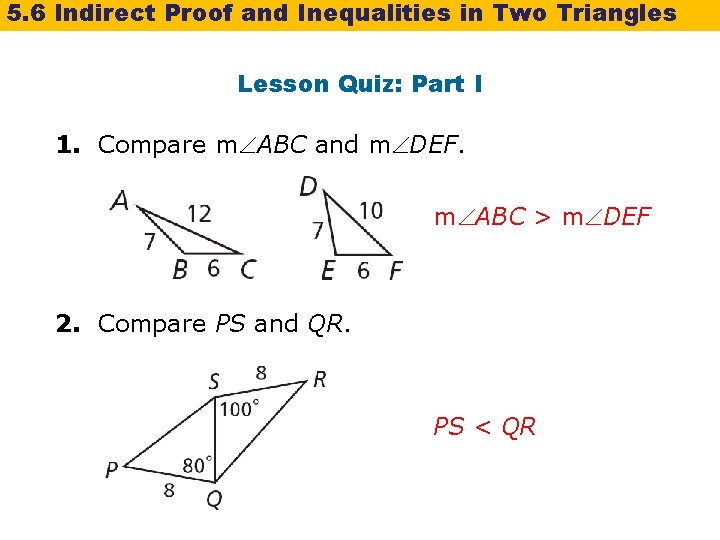
5. 6 Indirect Proof and Inequalities in Two Triangles Lesson Quiz: Part I 1. Compare m ABC and m DEF. m ABC > m DEF 2. Compare PS and QR. PS < QR
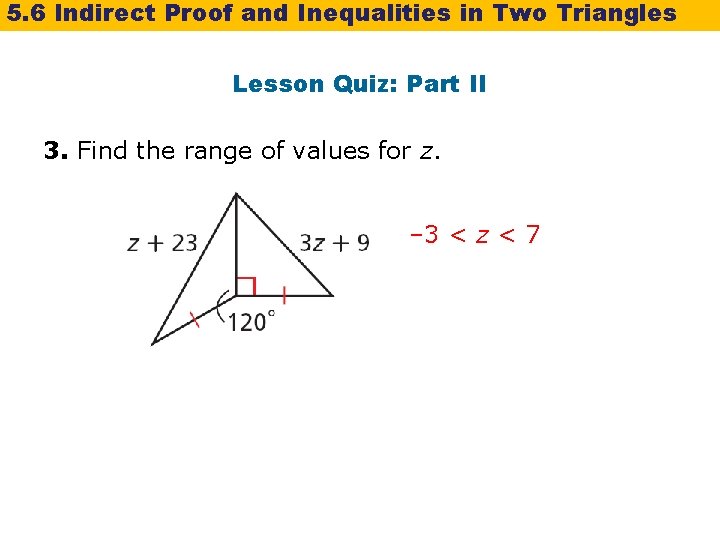
5. 6 Indirect Proof and Inequalities in Two Triangles Lesson Quiz: Part II 3. Find the range of values for z. – 3 < z < 7
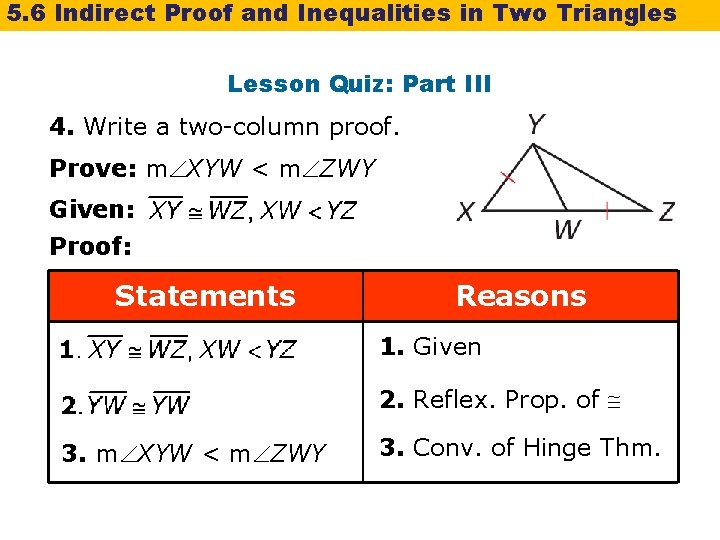
5. 6 Indirect Proof and Inequalities in Two Triangles Lesson Quiz: Part III 4. Write a two-column proof. Prove: m XYW < m ZWY Given: Proof: Statements Reasons 1. Given 2. Reflex. Prop. of 3. m XYW < m ZWY 3. Conv. of Hinge Thm.
Source: https://slidetodoc.com/5-6-inequalities-in-two-triangles-warm-up-2/
0 Response to "5 6 Inequalities in Two Triangles and Indirect Proof Continued"
Post a Comment